Геометрия 7 Мерзляк С-13-14 В1

Самостоятельная работа № 13-14 по геометрии в 7 классе «Параллельные прямые. Признаки параллельности двух прямых» с ответами в 4 вариантах (упражнения 89-96, вариант 1). Дидактические материалы предназначены для организации обучения по курсу планиметрии в массовой школе по учебнику «Геометрия 7 класс» А.Г.Мерзляк и др. Ответы на задания адресованы родителям, учителям, а также учащимся на дистанционном обучении. Код материалов: Геометрия 7 Мерзляк С-13-14 В1.

Вернуться к списку Самостоятельных работ (ОГЛАВЛЕНИЕ)

Геометрия 7 класс (Мерзляк)
Самостоятельная № 13. Вариант 1

Тема: Параллельные прямые

Параллельные прямые. Две прямые называют параллельными, если они не пересекаются.
Основное свойство параллельных прямых (аксиома параллельности прямых): Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Геометрия 7 класс (Мерзляк)
Самостоятельная № 14. Вариант 1

Тема: Признаки параллельности двух прямых

• Две прямые, перпендикулярные третьей прямой, параллельны.
• Если накрест лежащие углы, образующиеся при пересечении двух прямых секущей, равны, то прямые параллельны.
• Если сумма односторонних углов, образующихся при пересечении двух прямых секущей, равна 180°, то прямые параллельны.
• Если соответственные углы, образующиеся при пересечении двух прямых секущей, равны, то прямые параллельны.

Геометрия 7 Мерзляк С-13-14 В1
ОТВЕТЫ на ВАРИАНТ 1

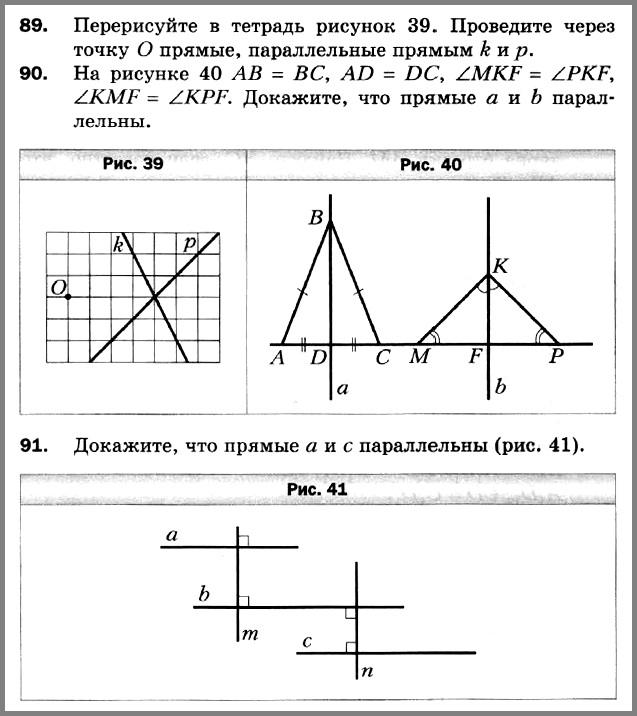
№ 89. Перерисуйте в тетрадь рисунок 39. Проведите через точку О прямые, параллельные прямым k и р.
ОТВЕТ: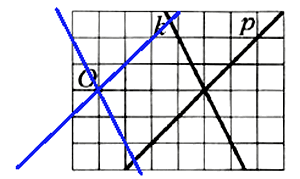

№ 90. На рисунке 40 АВ = ВС, AD = DC, ∠MKF = ∠PKF, ∠KMF = ∠KPF. Докажите, что прямые а и b параллельны.
ОТВЕТ: 1) AD = DC; AB = BC  => △ABC – равнобедренный
и BD – медиана  => BD – высота  => a ⊥ AC.
2) ∠MKF = ∠PKF; ∠KMF = ∠KPF  => △MKP – равнобедренный
и KF – биссектриса  => KF – высота  => b ⊥ MP.
3) Из 1 и 2  => a || b.

№ 91. Докажите, что прямые а и с параллельны (рис. 41).
ОТВЕТ: 1) b ⊥ m  и b ⊥ n  => m ⊥ n;
2) a ⊥ m и  a ⊥ n  => a || c.

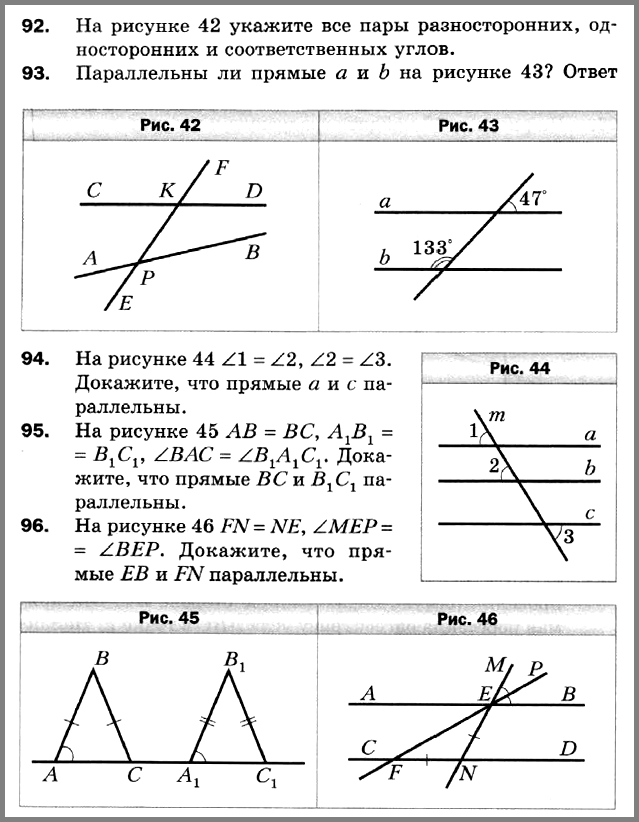
№ 92. На рисунке 42 укажите все пары разносторонних, односторонних и соответственных углов.
ОТВЕТ: 1) разносторонние углы: ∠PKO и ∠APK; ∠CKP и ∠KPB; ∠FKD и ∠APE; ∠CKF и ∠EPB;
2) односторонние углы: ∠DKP и ∠KPB; ∠CKP и ∠APK; ∠FKD и ∠EPB; ∠FKC и ∠APE;
3) соответственные углы: ∠FKD и ∠KPB; ∠FKC и ∠APK; ∠DKP и ∠EPB; ∠CKP и ∠APE.

№ 93. Параллельны ли прямые а и b на рисунке 43? Ответ обоснуйте.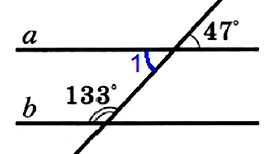

ОТВЕТ: 1) ∠1 -= 47° (вертикальные)
2) ∠1 + 133° = 47° + 133° = 180° (односторонние)  => a || b.

№ 94. На рисунке 44 ∠1 = ∠2, ∠2 = ∠3. Докажите, что прямые а и с параллельны.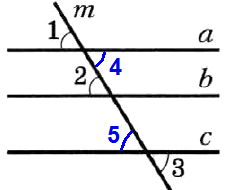

ОТВЕТ: 1) ∠1 = ∠2 и ∠2 = ∠3 (по условию) => ∠1 = ∠3;
2) ∠1 = ∠4 (вертикальные);
∠3 = ∠5 (вертикальные);
3) ∠1 = ∠3  => ∠4 = ∠5 (накрест лежащие)  => a || c.

№ 95. На рисунке 45 АВ = ВС, А₁В₁ = B₁C₁, ∠BAC = ∠B₁A₁C₁. Докажите, что прямые ВС и В₁С₁ параллельны.
ОТВЕТ: 1) AB = BC  => △ABC – равнобедр.  => ∠BAC = ∠BCA;
2) A₁B₁ = B₁C₁  => △A₁B₁C₁ – равнобедр.   => ∠B₁A₁C₁ = ∠B₁C₁A₁;
3) ∠BAC = ∠B₁A₁C₁ и ∠BAC = ∠BCA и ∠B₁A₁C₁ = ∠B₁C₁A₁  => ∠С = ∠С₁ (соответственные)
4) AC и A₁C₁ принадлежат прямой AC₁; △ABC ~ △A₁B₁C₁ => BC || B₁C₁.

№ 96. На рисунке 46 FN = NE, ∠MEP = ∠BEP. Докажите, что прямые ЕВ и FN параллельны.
ОТВЕТ: 1) FN = NE  => △FNE – равнобедренный => ∠EFN = ∠FEN;
∠FNE = 180° – ∠EFN – ∠FEN;
2) ∠MEP = ∠FEN (вертикальные) => ∠PEB = ∠FEN  = ∠NEB = 180° – ∠EFN – ∠ FEN;
3) Из 1 и 2 следует, что ∠FNE = ∠NEB (накрест лежащие) => ЕВ || FN.

Вернуться к списку Самостоятельных (в ОГЛАВЛЕНИЕ)

Вы смотрели: Самостоятельная работа по геометрии в 7 классе «Параллельные прямые. Признаки параллельности двух прямых» с ответами (1-й вариант из 4-х). Дидактические материалы адресованы родителям, учителям, а также учащимся на дистанционном обучении.